Obertöne und Naturtonreihe

Wie bei der Einführung in die Instrumentenkunde genauer erläutert, ist der Ton eines Musikinstrumentes gar kein einzelner Ton, sondern neben dem eigentlichen Ton (=Grundton) erklingen eine Reihe weiterer, höherer Töne, Obertöne genannt. Die Tonhöhe wird in Hertz gemessen (Abkürzung: Hz): je größer die Zahl ist, desto höher klingt der Ton.

Bei Saiten- und Blasinstrumenten sind die erklingenden Obertöne harmonisch, d.h. die Frequenzen der Obertöne sind ganzzahlige Vielfache der Frequenz des Grundtones (also hier im Beispiel 2x100, 3x100, 4x100 usw.).

Schreibt man die Obertöne der Reihe nach nebeneinander auf, ergibt sich die Naturtonreihe. Als Beispiel für die Naturntonreihe nehmen wir einmal den Ton c und nehmen an, er hätte eine Frequenz von 100 Hz. Tatsächlich hat c eine Frequenz von so etwa 130 Hz, aber wir wollen ja nicht Kopfrechnen üben, sondern die Musik verstehen.

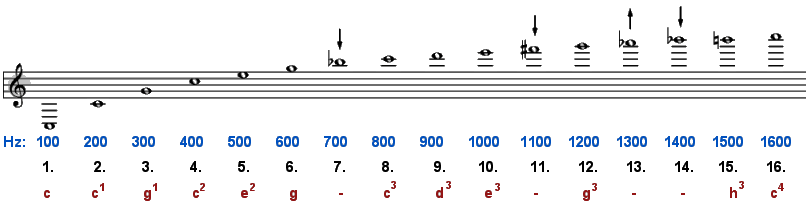
Obwohl die Frequenzen gleichmäßig ansteigen, werden die Abstände der Töne zueinander nach oben jedoch immer geringer.
Die durch Pfeile gekennzeichneten Töne lassen sich in unserem Notensystem nicht richtig darstellen und sind entsprechend höher oder tiefer. Da sich die Naturtonreihe theoretisch beliebig fortsetzen läßt, können so theoretisch alle Töne unseres Tonsystems entstehen.

Oktave

Wenn man die Frequenz eines Tones verdoppelt, entsteht ein Ton, der als "gleichartig" zum ersten Ton wahrgenommen wird. Diese gleichklingenden Töne erhalten in unserem Notensystem deshalb auch die gleichen Namen. Der Abstand zwischen ihnen wird als Oktave bezeichnet. Die Oktave findet man in der Naturtonreihe nicht nur zwischen 1. und 2. Naturton, sondern auch zwischen 2. und 4. (c1-c2), zwischen 3. und 6. usw.

Quinte

Betrachtet man das Intervall zwischen zweiten und dritten Ton, stellt man fest, daß die Frequenz letzteren Tones 1,5mal so hoch ist wie des ersteren. Anders ausgedrückt: das Verhältnis der Frequenzen ist 3:2 (dreifache Frequenz des Grundtones und doppelte Frequenz des Grundtones). Dieses Intervall heißt Quinte und klingt auch noch sehr harmonisch.

Quarte und Terz

Weiter geht es analog mit den Intervallen

• Quarte: Frequenzverhältnis 4:3, zwischen 4. und 3. Naturton
• große Terz: 5:4
• kleine Terz: 6:5

Der siebte Ton der Naturtonreihe klingt tiefer als in den Noten notiert, er existiert in unserem Notensystem nicht, und damit auch nicht der Abstand zwischen 7. und 6. Ton und auch nicht zwischen 8. und 7. Ton.

Sekunde

Danach folgen wieder Töne, die so exakt in unserem Tonsystem nicht vorkommen, und die Intervalle zwischen den Tönen werden ganz langsam immer kleiner, bis schließlich zwischen 16. und 15. Ton eine kleine Sekunde entsteht (Frequenzverhältnis 16:15).

Ein Halbton (=kleine Sekunde) ist nicht zu verwechseln mit dem "kleinen Ganzton" (=große Sekunde!).

Die übrigen Intevalle

Die restlichen Intervalle findet man zwischen mehreren Tönen:

• die große Sexte: zwischen 5. und 3. Ton, Frequenzverhältnis 5:3
• die kleine Sexte: 8:5
• die kleine Septime: 9:5
• die große Septime: 15:8

Noch einmal alle Intervalle im Überblick:

Intervall	Beispiel von c aufwärts	Frequenzverhältnis
Oktave		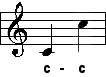2:1
Quinte		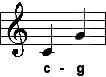3:2
Quarte		4:3
große Sexte		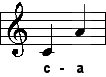5:3
große Terz		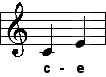5:4
kleine Terz		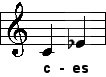6:5
kleine Sexte		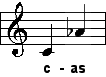8:5
kleine Septime		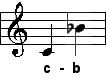9:5
große Sekunde		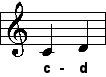9:8 oder 10:9
große Septime		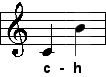15:8
kleine Sekunde		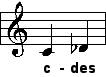16:15
Tritonus		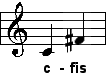45:32

Die Verhältniszahlen werden immer größer und gleichzeitig wird der Klang dissonanter, spätestens wenn die Zahlen über 8 steigen (also ab der Septime) spricht man von einem dissonanten Klang. Dieser Klang reibt im Ohr und erzeugt eine Spannung, man wünscht sich eine "Auflösung" zu einem konsonanten Klang.

Seite erstellt: 19.09.2007, letzte Änderung: 24.10.2007

Kopie von Musikzeit (www.musikzeit.de), Version vom 24.10.2007